Panpipes
 

Welcome to my page on panpipes!  It's designed for middle and high school science students who are interested in studying the physics of flutes.  On this page, you will find a short introduction on panpipes; a description on how they produce sound; and a demonstration on how to apply physics principles to this instrument – this section is particularly relevant for Science Olympiad participants in the Sounds of Music event.

Introduction

Panpipes, or pan flutes, can be traced to Greek mythology, Mayans, Native Americans, and many other ancient cultures [21].  These instruments are characterized by closed-end tubes of graduated length, and are constructed from traditional materials such as bamboo, oak, reeds, and river cane.  The panpipes that are demonstrated on this page are constructed from 1/2-inch schedule-40 PVC, with pennies glued onto the ends.  In terms of classification, panpipes are considered aerophones according to the Sachs-Hornbostel system, or in orchestral terminology, are considered part of the woodwind family of instruments. 

How It Works

What actually happens when a flute produces a sound, and how does it work?  We'll start by addressing this question. 

Panpipes, like all other flutes, produce their sound by vibrating a column of air inside of a tube.  Stated another way, what you hear is not the flute, but a vibrating column of air inside of the flute. 

In this section, we are going to look at this vibrating column of air: how it starts with something called an air jet, how it is shaped by the open and closed ends of the tube, and how it is stabilized into a constant pitch that is recognizable to our ears.

If you are a middle school student, the animations and videos below will probably be sufficient.  For high school students, I've also included additional text that is consistent with a high school physics textbook.  Lastly, for college-level physics students, it is important to note that sound waves are the result of both acoustic pressure and acoustic flow, which are 90 degrees out of phase with each other.  However, for the purposes of this web site, I will simply address the acoustic flow or the amplitude of motion of the air [5].  This will provide an approach that is consistent with current high school science curriculum.

Air Jet:

When a musician blows across a flute opening, whether a panpipe or a transverse flute, the airstream forms what is called an air jet. This air jet cycles through four phases, which can be seen in the animation below.  During these phases, forces are placed upon air particles that cause them to have a specific velocity, or a specific speed and direction of motion.  These velocities are referred to as the wave's acoustic velocity, and either pull the air downward or push the air upward.  In the first phase, the airstream splits on the inside edge of the panpipe.  Part of the air flows across the tube, and part of the air flows into the tube.  The part that flows into the tube creates a downward acoustic velocity, a downward pull of air particles into the tube.  As this motion increases, eventually all of the airstream flows into the tube, which marks the beginning of

How Panpipes Work

phase two.  At this point, a compression forms and begins a longitudinal wave.  As more air fills up the tube, some air particles begin to flow across the tube, and the airstream splits, which brings about phase three.  Once again, part of the air flows downward into the the tube, and part of the air flows across the tube.  This time, the part that flows across the tube creates an upward acoustic velocity, an upward push of air particles.  As this motion increases, eventually all of the airstream flows across the tube, which marks phase four.  In this final phase, a rarefaction is formed that continues the longitudinal wave.  [2 pg. 284-285, 4].

Reflection and Oscillation:

When the first compression (shown in blue) reaches the bottom of the tube it undergoes a fixed-end reflection, because the panpipe tube has a stopped end.  With fixed-end reflections such as these, compressions reflect back as rarefactions, and rarefactions as compressions [3]. Therefore, the first rarefaction creates a reflected compression wave traveling up the tube, as shown on the right.  As this pattern of reflections occurs at the stopped-end, an inverted longitudinal wave of reflected compressions travels up the tube, providing constructive interference with the incident compressions traveling down the tube.

A note on interference: The two major types of interference that occur are constructive and destructive.  When compressions meet rarefactions, destructive interference occurs.  However, when reflected compressions meet incident compressions, constructive interference occurs [17].

When a reflected compression (shown in red) reaches the top of the tube, it undergoes a free-end reflection, because the top of the tube is open.  With free-end reflections, compressions are reflected as compressions, and rarefactions as rarefactions [16]. Therefore, when the reflected compression reaches the top and reflects, it is in phase with the newly made compression, providing constructive interference that strengthens and stabilizes the wave pattern [1, pg. 390].

Standing wave:

Once the wave pattern is stabilized it is known as a standing wave. The areas of constructive interference become the antinodes of the wave, while the areas of destructive interference become the nodes [7, pg. 110-111].  As shown above, the panpipe is vibrating with a standing wave pattern of three antinodes and three nodes. This indicates that it is vibrating at the 5th harmonic.  Because it has a closed or stopped end, it can only vibrate at odd harmonics, such as the 1st harmonic or fundamental, the 3rd harmonic, or the 5th harmonic.  To see and hear a demonstration on harmonics and many other topics, please continue down the page.

Demonstrating What You Know

Now that we understand how panpipes produce sound, let's continue by exploring four more areas: frequency, amplitude, wavelength, and harmonics.

Frequency:

Frequency is simply a mathematical representation of how low or high a pitch is, and is based on the rate at which waves vibrate [15, pg. 8].  It is measured in Hertz, or number of complete wave cycles per second, and is commonly abbreviated as Hz [18].  Since sound is produced on panpipes by a vibrating column of air, the amount of time it takes for one compression to travel down and up the tube will determine its frequency.  To see how frequency can be demonstrated on a set of panpipes, start the video below.

If we change the length of a tube, we also change the length of the air column inside of that tube.  Simply put: shorter is higher, and longer is lower.  But it's actually more precise than that.  The Fundamental Principal states that each time we cut the length in half, we double the frequency.  Stated another way: tube length and frequency are inversely proportional [15, pg. 10]. 

This Fundamental Principle is demonstrated with the animation on the right.  One panpipe has a length that is equal to 1 unit, while the other tube is 1/2 of that length.  Imagine that sound, as represented by the arrow, is the motion of a longitudinal wave traveling down the tube and then reflecting back.  Notice how sound waves travel the length of the shorter tube twice as fast as the longer tube.  Sound waves complete two cycles with the shorter tube in the time it takes to complete one cycle with the longer tube.  As a result, when tube length is halved, frequency is doubled [15, pg. 10]. 

Amplitude:

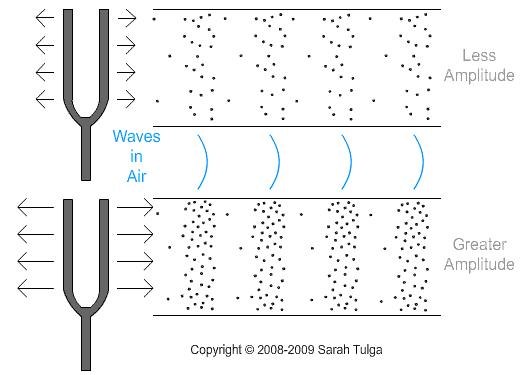
Amplitude is the variation or displacement of a wave from its mean value.  With sound waves, it is the extent to which air particles are displaced, and is experienced as the intensity or loudness of a sound.   As shown below,  when a tuning fork vibrates to a greater degree, it displaces more air particles in each compression.  When the tuning fork vibrates to a lesser degree, it displaces fewer air particles in each compression. 

Amplitude can be changed on panpipes by simply varying the amount of air in your playing technique.  Playing softly, with less air, will produce less amplitude.  Taking a deep breath and playing with more air, will produce greater amplitude.

Varying Amplitude

 

Wavelength:

Wavelengths on a Closed-end Tube: Fundamental or 1st harmonic, 3rd harmonic, and 5th harmonic

In determining the wavelength of a tube, it is important to know if the tube has two open ends, or one open end and one closed end.  With panpipes, the tubes all have one open end, and one closed end.  

Since one end is closed, the wavelength of the fundamental frequency is four times the length of the tube [6, pg. 250].  This is because the closed or stopped end always serves as a node when the tube resonates in a standing wave pattern.  The opposite effect occurs at the open end, which always serves as an antinode [7, pg. 111].

Therefore, if we superimpose a transverse wave over the tube (as shown in the adjacent figure) one complete wave cycle extends four times the length of the tube.  This represents the fundamental frequency for the tube, or the lowest resonant frequency that the tube can produce.   Again, notice the relationship between the tube's closed and open ends, and the wave's nodes and antinodes.  We can see the same relationship with the third and fifth harmonics.  Also, notice how wavelengths are shorter with higher frequencies.   To see more on the topic of wavelength for open and closed-end tubes, please also see my Harmonics Activity.

Harmonics and Timbre:

When the air vibrates inside of a panpipe tube, it resonates in fractional vibrations called Harmonics.  Because of this phenomenon, there is an interesting relationship between wavelength and frequency – one that relates to the Fundamental Principal [15, pg. 10]. 

Let's start with the first harmonic.  It's also called the fundamental and it has a wavelength as shown above.  Now when we look at the third harmonic, we see that its wavelength is only 1/3 of the fundamental, while its frequency is tripled.  Similarly, the wavelength of the fifth harmonic is 1/5 of the fundamental, and its frequency is multiplied by five.  This shows an important characteristic of panpipes: they vibrate in fractions and produce harmonics – multiples of the fundamental frequency.   And as we learned in the previous section, since panpipes are closed or stopped at one end, they can only play odd harmonics [3].  To hear how to obtain these harmonics, please play the video on the right.

After we understand harmonics, we can apply it to the musical concept of timbre or tone.   Timbre (pronounced tam-ber) refers to the quality or tonal color of a sound, and it is determined by which harmonics are simultaneously present in the sound.  In order to produce a change in timbre, one simply overblows the tube slightly to mix in the 3rd or 5th harmonics, thereby producing a composite sound in which harmonics become a controllable variable for musical effect [6, pg. 249]. 

Many people believe that the tube material will drastically change the timbre or tone of the instrument.  However, as commonly held as that might be, it is false.  According to Coltman's (1971) experiments, there is no audible distinction between flutes made of different materials: ranging from cardboard to copper [1, pg. 460, 2, pg. 295].  The only source of timbre or tonal differences come from changes in the embouchure hole, or in transverse flutes the head joint, as well as changes in the resonating tube dimensions [1, pg. 460, 2, pg. 295].  This lack of distinction is because the sound is being produced by a vibrating column of air inside of the tube, not the actual tube itself. 

Works Cited